【递归】汉诺塔问题

题目描述：

楚继光报怨道：“能量盘为什么要这样移动？真够麻烦的。”

“因为这样移动，暗含宇宙运行的奥义，它能够产生巨大的魔法力，将修罗王的魔法炮阵灭成渣。”墨老师一副高深莫测的神情。

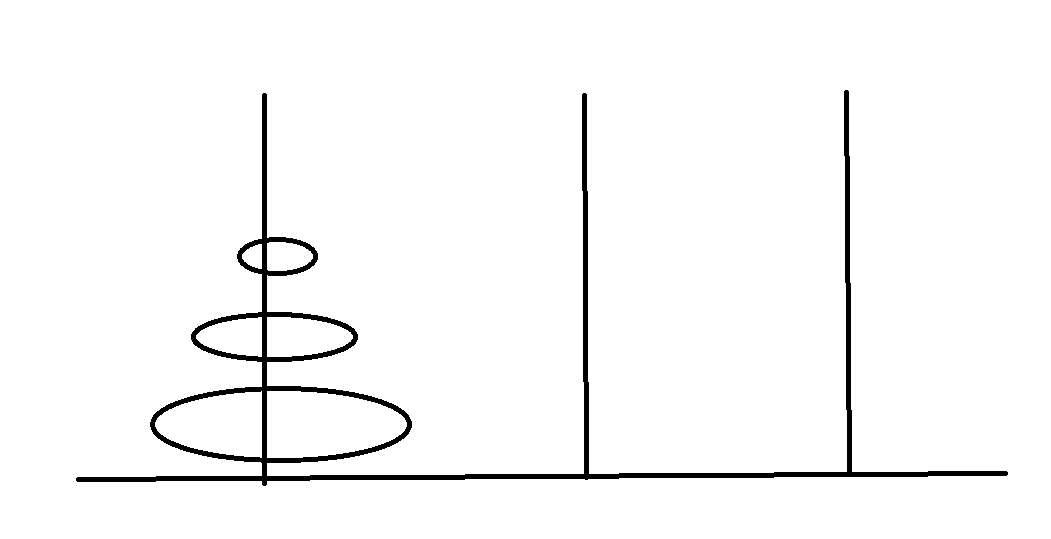
如图所示，已知魔法学院的防御系统的能量模块上有三根柱子a，b，c，能量盘为中间有孔的圆盘状，能量盘直径依次递减，初始时b柱、c柱为空，所有盘片套在a柱上，并且上面的盘片总是比下面的盘片小，现需将a柱上的能量盘通过b柱移到c柱上，规则是每次移动只能移动最上面的能量盘，而且保持任何柱子上的能量盘的排列均是上面的盘片比下面的盘片要小。试问需要移动多少次？

输入格式：

一个整数n，表示n个盘。

输出格式：

一个整数，表示需要移动的次数。

输入样式：

2

输出样式

3

解题思路：

将A盘子上N个盘子移动到C盘子可以分解成将A盘子上N-1个盘子通过C移动到B上面，再将A上一个盘子移动到C上面，再将B上面的N-1个盘子通过A移动到C;

AC代码：

#include<iostream>
using namespace std;
int num=0;//移动次数
void hanci(int n,char a,char b,char c){//n代表a柱子上的剩余盘子数 
	if(n==1){
		cout<<a<<"->"<<c<<endl;
		return;
	}
	hanci(n-1,a,c,b);
	cout<<a<<"->"<<c<<endl;
	hanci(n-1,b,a,c);
} 
int main() {
	int n;
	cin>>n;
	hanci(n,'A','B','C');
}